Når to eller flere lydbølger er til stede samtidig, blandes lydbølgerne til en ny lydbølge. Man siger, at lydbølgerne interfererer med hinanden. Fænomenet kaldes interferens.
Indhold
1. Konstruktiv og destruktiv interferens
Konstruktiv interferens opstår, når lydbølger forstærker hinanden. Forstærkningen sker, når lydbølgerne er i fase, dvs. når lydbølgernes udsving (bølgetoppe og bølgedale) følges ad. Hvis bølgetoppene og bølgedalene indtræder på eksakt samme tidspunkt, siger man, at faseforskellen er 0° (0 grader). Resultatet bliver en lydbølge med en amplitude, der er lig summen af de tilstedeværende lydbølgers amplituder.
Her er en illustration af to lydbølger på 440 Hz med en amplitude på henholdsvis 1,1 (sort lydbølge) og 0,5 (grøn lydbølge). Lydbølgernes faseforskel er 0°:

440 Hz (1,1)
440 Hz (0,5)
Resultatet bliver en lydbølge på 440 Hz med en amplitude på 1,1 + 0,5 = 1,6:

Destruktiv interferens opstår, når lydbølger svækker hinanden. Svækkelsen sker, når lydbølgerne er i modfase, dvs. når lydbølgernes udsving (bølgetoppe og bølgedale) er modsatrettede. Hvis bølgetoppene og bølgedalene indtræder eksakt modsat hinanden, siger man, at faseforskellen er 180°. Resultatet bliver en lydbølge med en amplitude, der er lig differencen mellem de tilstedeværende lydbølgers amplituder.
Her er en illustration af to lydbølger på 440 Hz med en amplitude på henholdsvis 1,1 (sort lydbølge) og 0,3 (grøn lydbølge). Lydbølgernes faseforskel er 180°:

440 Hz (1,1)
440 Hz (0,3)
Resultatet bliver en lydbølge på 440 Hz med en amplitude på 1,1 - 0,3 = 0,8:

Det er imidlertid mere sandsynligt, at to lydbølger hverken er i eksakt fase eller eksakt modfase, men et sted midt imellem. Her er en illustration af to lydbølger på henholdsvis 440 Hz (sort lydbølge) og 880 Hz (grøn lydbølge) med en amplitude på henholdsvis 1,5 og 1,2:

440 Hz
840 Hz
Når de to lydbølger er i fase, bliver amplituden større (konstruktiv interferens), og når de to lydbølger er i modfase, bliver amplituden mindre (destruktiv interferens). Resultatet bliver derfor en forskubbet og lidt forstærket lydbølge, som indeholder begge frekvenser (440 Hz og 880 Hz):
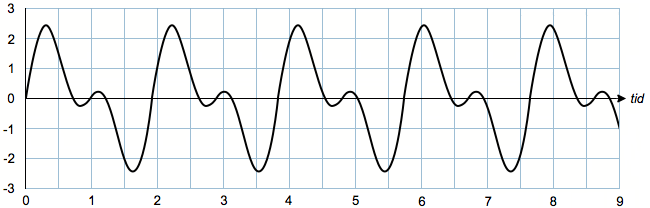
To identiske toner med identisk amplitude i eksakt modfase kan i princippet udslukke hinanden fuldstændigt, så de ikke kan høres. Man kan eksempelvis forestille sig, at to violinister i et orkester spiller den samme tone med den samme lydstyrke, men forskudt i tid, så lydbølgerne er i eksakt modfase. Amplituden vil da være lig nul, og tonen vil ikke kunne høres.
I praksis er det dog umuligt, blandt andet fordi det er meget usandsynligt, at de to toner frembringes i eksakt modfase. Tilsvarende er det meget usandsynligt, at violinisterne spiller i eksakt fase, og derfor fordobles lydstyrken ikke, selvom antallet af violinister fordobles.
Lytteøvelse 40
Lyt til konstruktiv og destruktiv interferens fra en stemmegaffel:
- Find en stemmegaffel. De to spidser på stemmegaflen kan anskues som to svingende legemer, der frembringer hver sin identiske tone.
- Anslå stemmegaflen, hold den lodret op til øret, og drej den langsom rundt.
- Du vil bemærke, at lydstyrken stiger og falder, når du drejer stemmegaflen rundt. Det skyldes, at der er områder omkring stemmegaflen, hvor lydbølgerne fra de to svingende legemer er i fase (konstruktiv interferens), og områder hvor de er i modfase (destruktiv interferens).
- I hvilke områder omkring stemmegaflen er der konstruktiv interferens?
Tænk og diskuter 13
Støjreducerende hovedtelefoner bruger destruktiv interferens til at dæmpe baggrundsstøj. Hovedtelefonerne er forsynet med små mikrofoner, som opfanger den omgivende støj. En processor analyserer støjen, skaber en kopi af den og afspiller kopien i modfase. Derved udligner de to lydkilder mere eller mindre hinanden, og støjen kan i nogle tilfælde reduceres helt op til 70%.
Teknologien virker kun på monotone baggrundslyde som eksempelvis motorstøj. I hvilke tilfælde kan man bruge destruktiv interferens til at dæmpe lyd?
2. Stødtoner
Stødtoner (også kaldet svævninger) opstår, når to lydbølger med lidt forskellig frekvens interfererer med hinanden. Stødtonernes frekvens stødfrekvensen er lig med differencen mellem de to lydbølgers frekvens. Man kan altså opstille følgende formel: fstød = f2 - f1.
To lydbølger på henholdsvis 400 Hz og 402 Hz skaber stødtoner med en frekvens på 2 Hz. Stødtonerne kan høres som en række kontinuerlige udsving i lydstyrken - i dette tilfælde to udsving per sekund (2 Hz), svarende til to stødtoner per sekund. Selve tonen på 2 Hz opstår ikke, og stødtoner er derfor ikke egentlige toner men blot udsving i lydstyrken.
Stødtonerne kan kun høres, hvis frekvensforskellen mellem lydbølgerne er forholdsvis lille. Hvis frekvensforskellen er stor, kan stødtonerne ikke høres, fordi man da blot vil opfatte lydbølgerne som to forskellige toner (og ikke én tone med udsving i lydstyrken).
Her er en illustration af to lydbølger på henholdsvis 110 Hz og 115 Hz:
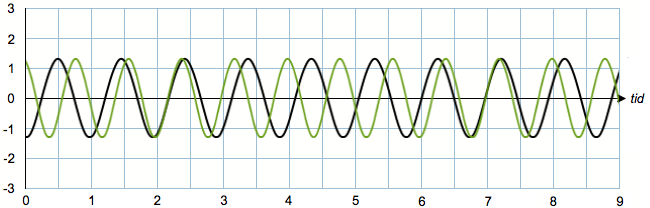
110 Hz
115 Hz
Når lydbølgerne er i fase, bliver amplituden større (konstruktiv interferens), og når lydbølgerne er i modfase (midterst i billedet), bliver amplituden mindre (destruktiv interferens). Resultatet bliver derfor en lydbølge med en lydstyrke, der periodisk stiger og falder:
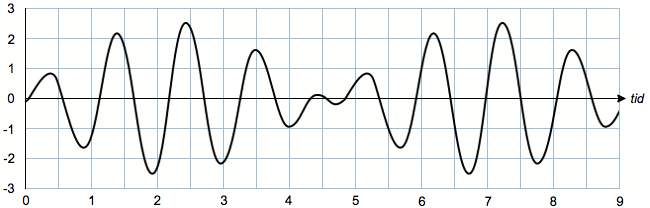
De periodiske udsving i lydstyrken er det, der opfattes som stødtoner. Stødtonernes frekvens er i dette tilfælde 5 Hz, fordi differencen mellem de to lydbølger er 5 Hz. Der forekommer altså fem stødtoner per sekund (hvoraf de to er illustreret på billedet).
På en harmonika udnytter man stødtonerne til at give harmonikaen en fyldigere klang. Hver tone er faktisk flere forskellige toner, der er stemt lidt forskelligt, og når de klinger samtidig, opstår der en fyldig og vibrerende klang fra stødtonerne.
Lytteøvelse 41
Frembring stødtoner ved hjælp af to tonegeneratorer:
- Åben to tonegeneratorer her (åbner i nyt vindue).
- Sæt den øverste tonegenerator til 341 Hz og den nederste til 340 Hz. Lyt til tonerne hver for sig, og lyt derefter til dem samtidig. Når du lytter til tonerne samtidig, kan du høre én stødtone per sekund, fordi frekvensforskellen mellem tonerne er 1.
- Øg frekvensen i den øverste tonegenerator langsomt (marker tallet, og tryk 'pil op' på tastaturet), så antallet af stødtoner per sekund øges. Ved hvilken frekvens kan du ikke længere høre nogen stødtoner?
Lytteøvelse 42
Når man skal stemme strengeinstrumenter uden brug af elektroniske hjælpemidler, udnytter man ofte stødtoner til at stemme strengene helt præcist. Prøv at stemme to strenge på en guitar ved hjælp af stødtoner:
- Find en guitar, der ikke stemmer.
- Lad venstre hånds pegefinger (højre hånd, hvis du er venstrehåndet) hvile let på 2. streng umiddelbart over 5. bånd. Anslå strengen med den anden hånd så langt nede ved stolen som muligt. Du kan nu høre en lys såkaldt flageolettone.
- Anslå straks derefter 3. streng, mens du lader din ringfinger hvile let over strengens 7. bånd. Du kan nu høre samme lyse flageolettone som før.
- Hvis strengene ikke er stemt helt rene, kan du høre et antal stødtoner mellem de to flageolettoner. Ved at justere den ene strengs anspændthed (ved hjælp af stemmeskruen på guitarens hoved) kan du stemme strengen, og stødtonerne vil da blive langsommere og til sidst forsvinde helt.
- Når stødtonerne er forsvundet, er frekvenserne af de to flageolettoner ens, og dermed er strengene stemt helt rene.
3. Kombinationstoner
Kombinationstoner er svagtklingende toner, som i nogle tilfælde opstår, når to forskellige toner klinger samtidig. Kombinationstoner har ikke nogen reel eksistens, men er et fysiologisk indbildningsfænomen, der opstår ved lydbølgernes passage i øret.
Man skelner mellem differenstoner og summationstoner. Differenstoner har en frekvens, der er lig med differencen mellem de to toners frekvenser. Summationstoner har en frekvens, der er lig med summen af de to toners frekvenser. To toner på henholdsvis 800 Hz og 600 Hz skaber således en differenstone på 200 Hz og en summationstone på 1400 Hz.
Differenstoner har været kendt siden starten af 1700-tallet, men den første beskrivelse stammer fra den italienske violinist Guiseppe Tartini (1692-1770) i 1754. Generelt høres differenstoner bedst ved kraftig lydstyrke og ved brug af sinustoner. Naturligt frembragte toner er sammensat af mange forskellige lyde (blandt andet lydene fra de mekaniske dele på musikinstrumentet), og disse lyde gør det svært at høre differenstonerne. Summationstoner kan kun meget sjældent høres.
Herunder er tre eksempler på differenstoner, der opstår som følge af tre fuldstændigt rene intervaller. Differenstonerne er vist i nederste nodesystem, men de er meget svære at høre, fordi de mange klanglige nuancer i klaverlyden skjuler dem:

Læg mærke til, at en lille terts klinger som en dur-akkord, hvori differenstonen udgør akkordens grundtone. Det gælder dog kun, hvis intervallet er fuldstændigt rent. I den ligesvævende stemning er alle intervaller (undtagen oktaven) stemt en lille smule falske, og differenstonen til en lille terts er da næsten en halv tone for lav i forhold til grundtonen. Musikalsk set fungerer differenstoner derfor kun i sammenhænge, hvor man kan spille fuldstændigt rene intervaller (eksempelvis i strygergrupper). I praksis klinger differenstoner dog så lavt, at de er uden betydning.
Lytteøvelse 43
Demonstrer differenstoner ved hjælp af to tonegeneratorer:
- Tilslut et par gode hovedtelefoner til computeren.
- Åben to tonegeneratorer her (åbner i nyt vindue).
- Sæt den øverste tonegenerator til 1200 Hz og den nederste tonegenerator til 1000 Hz. Hvis du lytter godt efter, kan du høre en svag differenstone på 200 Hz. Afspil eventuelt først en tone på 200 Hz, så du er forberedt på, hvilken tone du skal lytte efter.
Lytteøvelse 44
Ved at kombinere forskellige toner i en særlig rækkefølge, kan man skabe melodier med differenstoner. Tilslut et par gode hovedtelefoner til computeren, og prøv, om du kan høre melodierne i de følgende to lydeksempler. Du skal lytte efter de dybt klingende differenstoner og forsøge at abstrahere fra de lyse toner, der danner differenstonerne.
USA's nationalmelodi The Star-Spangled Banner (John Stafford Smith, ca. 1773):
Europahymnen Ode to Joy (Ludwig van Beethoven, 1824):
I første lydeksempel dannes differenstonerne af lange, lyse toner, der følger melodirytmen. I sidste lydeksempel dannes differenstonerne af korte, lyse toner, der skifter vilkårligt 32 gange i sekundet.
Lytteøvelse 45
Nogle komponister udnytter bevidst differenstoner til at frembringe dybe toner, som ikke bliver spillet. Den danske komponist Per Nørgård har eksempelvis arbejdet med differenstoner i indledningen til operaen Gilgamesh (1972), hvor differenstonerne skabes som følge af en række elektroniske lyde.
Lyt til Gilgamesh her, og prøv, om du kan høre differenstonerne. De er meget svære (eller helt umulige) at høre - bedøm selv:
Når to eller flere lydbølger er til stede samtidig, blandes lydbølgerne til en ny lydbølge. Man siger, at lydbølgerne interfererer med hinanden. Fænomenet kaldes interferens.
Indhold
1. Konstruktiv og destruktiv interferens
Konstruktiv interferens opstår, når lydbølger forstærker hinanden. Forstærkningen sker, når lydbølgerne er i fase, dvs. når lydbølgernes udsving (bølgetoppe og bølgedale) følges ad. Resultatet bliver en lydbølge med en amplitude, der er lig summen af de tilstedeværende lydbølgers amplituder.
Her er en illustration af to lydbølger på 440 Hz med en amplitude på henholdsvis 1,1 (sort lydbølge) og 0,5 (grøn lydbølge):

440 Hz (1,1)
440 Hz (0,5)
Resultatet bliver en lydbølge på 440 Hz med en amplitude på 1,1 + 0,5 = 1,6:

Destruktiv interferens opstår, når lydbølger svækker hinanden. Svækkelsen sker, når lydbølgerne er i modfase, dvs. når lydbølgernes udsving (bølgetoppe og bølgedale) er modsatrettede. Resultatet bliver en lydbølge med en amplitude, der er lig differencen mellem de tilstedeværende lydbølgers amplituder.
Her er en illustration af to lydbølger på 440 Hz med en amplitude på henholdsvis 1,1 (sort lydbølge) og 0,3 (grøn lydbølge):

440 Hz (1,1)
440 Hz (0,3)
Resultatet bliver en lydbølge på 440 Hz med en amplitude på 1,1 - 0,3 = 0,8:

Det er imidlertid mere sandsynligt, at to lydbølger hverken er i eksakt fase eller eksakt modfase, men et sted midt imellem. Her er en illustration af to lydbølger på henholdsvis 440 Hz (sort lydbølge) og 880 Hz (grøn lydbølge) med en amplitude på henholdsvis 1,5 og 1,2:

440 Hz
840 Hz
Når de to lydbølger er i fase, bliver amplituden større (konstruktiv interferens), og når de to lydbølger er i modfase, bliver amplituden mindre (destruktiv interferens). Resultatet bliver derfor en forskubbet og lidt forstærket lydbølge, som indeholder begge frekvenser (440 Hz og 880 Hz):

To identiske toner med identisk amplitude i eksakt modfase kan i princippet udslukke hinanden fuldstændigt, så de ikke kan høres. Man kan eksempelvis forestille sig, at to violinister i et orkester spiller den samme tone med den samme lydstyrke, men forskudt i tid, så lydbølgerne er i eksakt modfase. Amplituden vil da være lig nul, og tonen vil ikke kunne høres.
I praksis er det dog umuligt, blandt andet fordi det er meget usandsynligt, at de to toner frembringes i eksakt modfase. Tilsvarende er det meget usandsynligt, at violinisterne spiller i eksakt fase, og derfor fordobles lydstyrken ikke, selvom antallet af violinister fordobles.
Lytteøvelse 40
Lyt til konstruktiv og destruktiv interferens fra en stemmegaffel:
- Find en stemmegaffel. De to spidser på stemmegaflen kan anskues som to svingende legemer, der frembringer hver sin identiske tone.
- Anslå stemmegaflen, hold den lodret op til øret, og drej den langsom rundt.
- Du vil bemærke, at lydstyrken stiger og falder, når du drejer stemmegaflen rundt. Det skyldes, at der er områder omkring stemmegaflen, hvor lydbølgerne fra de to svingende legemer er i fase (konstruktiv interferens), og områder hvor de er i modfase (destruktiv interferens).
- I hvilke områder omkring stemmegaflen er der konstruktiv interferens?
Tænk og diskuter 32
Støjreducerende hovedtelefoner bruger destruktiv interferens til at dæmpe baggrundsstøj. Hovedtelefonerne er forsynet med små mikrofoner, som opfanger den omgivende støj. En processor analyserer støjen, skaber en kopi af den og afspiller kopien i modfase. Derved udligner de to lydkilder mere eller mindre hinanden, og støjen kan i nogle tilfælde reduceres helt op til 70%.
Teknologien virker kun på monotone baggrundslyde som eksempelvis motorstøj. I hvilke tilfælde kan man bruge destruktiv interferens til at dæmpe lyd?
2. Stødtoner
Stødtoner opstår, når to lydbølger med lidt forskellig frekvens interfererer med hinanden. Stødtonernes frekvens stødfrekvensen er lig med differencen mellem de to lydbølgers frekvens.
To lydbølger på henholdsvis 400 Hz og 402 Hz skaber stødtoner med en frekvens på 2 Hz. Stødtonerne kan høres som en række kontinuerlige udsving i lydstyrken - i dette tilfælde to udsving per sekund (2 Hz), svarende til to stødtoner per sekund. Selve tonen på 2 Hz opstår ikke, og stødtoner er derfor ikke egentlige toner men blot udsving i lydstyrken.
Stødtonerne kan kun høres, hvis frekvensforskellen mellem lydbølgerne er forholdsvis lille. Hvis frekvensforskellen er stor, kan stødtonerne ikke høres, fordi man da blot vil opfatte lydbølgerne som to forskellige toner (og ikke én tone med udsving i lydstyrken).
Her er en illustration af to lydbølger på henholdsvis 110 Hz og 115 Hz:

110 Hz
115 Hz
Når lydbølgerne er i fase, bliver amplituden større (konstruktiv interferens), og når lydbølgerne er i modfase (midterst i billedet), bliver amplituden mindre (destruktiv interferens). Resultatet bliver derfor en lydbølge med en lydstyrke, der periodisk stiger og falder:

De periodiske udsving i lydstyrken er det, der opfattes som stødtoner. Stødtonernes frekvens er i dette tilfælde 5 Hz, fordi differencen mellem de to lydbølger er 5 Hz. Der forekommer altså fem stødtoner per sekund (hvoraf de to er illustreret på billedet).
På en harmonika udnytter man stødtonerne til at give harmonikaen en fyldigere klang. Hver tone er faktisk flere forskellige toner, der er stemt lidt forskelligt, og når de klinger samtidig, opstår der en fyldig og vibrerende klang fra stødtonerne.
Lytteøvelse 41
Frembring stødtoner ved hjælp af to tonegeneratorer:
- Åben to tonegeneratorer her (åbner i nyt vindue).
- Sæt den øverste tonegenerator til 341 Hz og den nederste til 340 Hz. Lyt til tonerne hver for sig, og lyt derefter til dem samtidig. Når du lytter til tonerne samtidig, kan du høre én stødtone per sekund, fordi frekvensforskellen mellem tonerne er 1.
- Øg frekvensen i den øverste tonegenerator langsomt (marker tallet, og tryk 'pil op' på tastaturet), så antallet af stødtoner per sekund øges. Ved hvilken frekvens kan du ikke længere høre nogen stødtoner?
Lytteøvelse 42
Når man skal stemme strengeinstrumenter uden brug af elektroniske hjælpemidler, udnytter man ofte stødtoner til at stemme strengene helt præcist. Prøv at stemme to strenge på en guitar ved hjælp af stødtoner:
- Find en guitar, der ikke stemmer.
- Lad venstre hånds pegefinger (højre hånd, hvis du er venstrehåndet) hvile let på 2. streng umiddelbart over 5. bånd. Anslå strengen med den anden hånd så langt nede ved stolen som muligt. Du kan nu høre en lys såkaldt flageolettone.
- Anslå straks derefter 3. streng, mens du lader din ringfinger hvile let over strengens 7. bånd. Du kan nu høre samme lyse flageolettone som før.
- Hvis strengene ikke er stemt helt rene, kan du høre et antal stødtoner mellem de to flageolettoner. Ved at justere den ene strengs anspændthed (ved hjælp af stemmeskruen på guitarens hoved) kan du stemme strengen, og stødtonerne vil da blive langsommere og til sidst forsvinde helt.
- Når stødtonerne er forsvundet, er frekvenserne af de to flageolettoner ens, og dermed er strengene stemt helt rene.
3. Kombinationstoner
Kombinationstoner er svagtklingende toner, som i nogle tilfælde opstår, når to forskellige toner klinger samtidig. Kombinationstoner har ikke nogen reel eksistens, men er et fysiologisk indbildningsfænomen, der opstår ved lydbølgernes passage i øret.
Man skelner mellem differenstoner og summationstoner. Differenstoner har en frekvens, der er lig med differencen mellem de to toners frekvenser. Summationstoner har en frekvens, der er lig med summen af de to toners frekvenser. To toner på henholdsvis 800 Hz og 600 Hz skaber således en differenstone på 200 Hz og en summationstone på 1400 Hz.
Differenstoner høres bedst ved kraftig lydstyrke og ved brug af sinustoner. Naturligt frembragte toner er sammensat af mange forskellige lyde (blandt andet lydene fra de mekaniske dele på musikinstrumentet), og disse lyde gør det meget svært at høre differenstonerne. Summationstoner kan kun meget sjældent høres.
Lytteøvelse 43
Demonstrer differenstoner ved hjælp af to tonegeneratorer:
- Tilslut et par gode hovedtelefoner til computeren.
- Åben to tonegeneratorer her (åbner i nyt vindue).
- Sæt den øverste tonegenerator til 1200 Hz og den nederste tonegenerator til 1000 Hz. Hvis du lytter godt efter, kan du høre en svag differenstone på 200 Hz. Afspil eventuelt først en tone på 200 Hz, så du er forberedt på, hvilken tone du skal lytte efter.
Lytteøvelse 44
Ved at kombinere forskellige toner i en særlig rækkefølge, kan man skabe melodier med differenstoner. Tilslut et par gode hovedtelefoner til computeren, og prøv, om du kan høre melodierne i de følgende to lydeksempler. Du skal lytte efter de dybt klingende differenstoner og forsøge at abstrahere fra de lyse toner, der danner differenstonerne.
USA's nationalmelodi The Star-Spangled Banner (John Stafford Smith, ca. 1773):
Europahymnen Ode to Joy (Ludwig van Beethoven, 1824):
I første lydeksempel dannes differenstonerne af lange, lyse toner, der følger melodirytmen. I sidste lydeksempel dannes differenstonerne af korte, lyse toner, der skifter vilkårligt 32 gange i sekundet.
Lytteøvelse 45
Nogle komponister udnytter bevidst differenstoner til at frembringe dybe toner, som ikke bliver spillet. Den danske komponist Per Nørgård har eksempelvis arbejdet med differenstoner i indledningen til operaen Gilgamesh (1972), hvor differenstonerne skabes som følge af en række elektroniske lyde.
Lyt til Gilgamesh her, og prøv, om du kan høre differenstonerne. De er meget svære (eller helt umulige) at høre - bedøm selv: